How Experts Lie (Part 2)

Anonymously?

---

Many parties are using this government of Canada article to justify their (over)reaction to COVID-19.

https://www.canada.ca/en/public-health/services/diseases/coronavirus-disease-covid-19/epidemiological-economic-research-data/excess-mortality-impacts-age-comorbidity.html

The authors are unknown, but their data is being used by people trying to make the case that COVID-19 was an extremely deadly pandemic for Canada.

Let’s look at their claims of “Excess Mortality”.

This famous government article says:

Well that’s reassuring! It’s a FACT SHEET !!!

• “Of the 309,912 total deaths observed in 2020, an estimated 16,333 excess deaths occurred (expected deaths: 295,379).”

• 16,333 / 309,912 = 5.27% “Excess Deaths”

Is it “exaggerated” to call 5.27% excess deaths in Canada a “Deadly” pandemic?

Was it really 5.27%?

Let’s look closer before jumping to conclusions.

First, it says: “estimated 16,333 excess deaths occurred..”

Can an “estimate” be called a FACT? (Isn’t this supposed to be a fact sheet?)

I am estimated to be 6 feet tall, but I am in fact 5’10”. Semantically, it looks like an Estimate cannot be a Fact.

(Maybe this “fact sheet” is really a “guess sheet”.)

If “estimate” means that in fact no people died, then are their estimates actually still alive?

(Variants of this existential question "Does an absence of death actually equal life?" may have been the loose thread that unraveled philosophy during the enlightenment into postmodernism today.¹)

More importantly, is it possible to find out if these “excess” deaths really died?

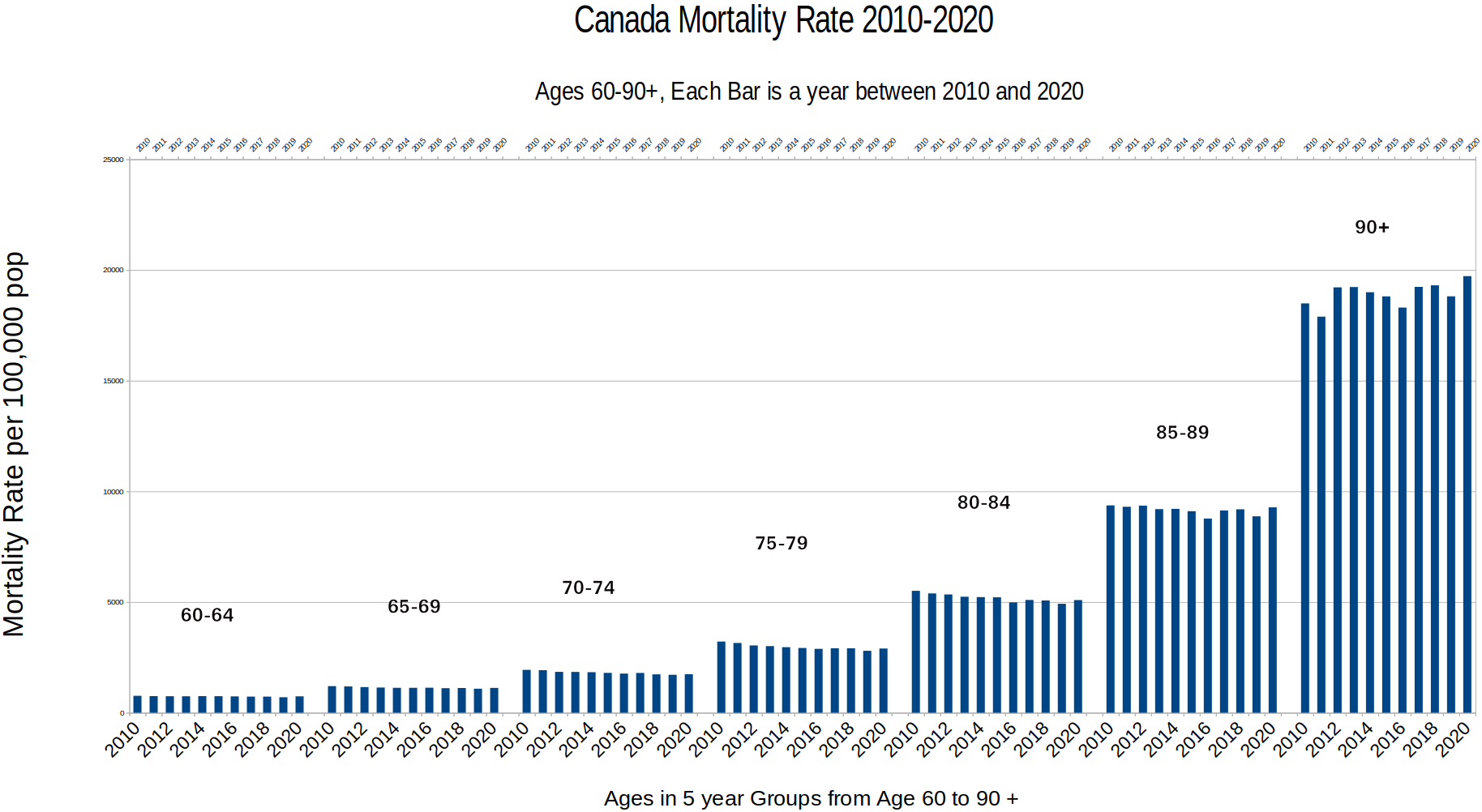
Actual death statistics instead of "estimates" would be a good starting point. Here's a graph I made of the mortality data from Statistics Canada from 2010-2020 .²

If the mortality rates are unchanged in 2020 compared with previous years, then the “Estimated Dead” must still be alive. That is, in the absence of a rise in rates of mortality, there cannot be any “excess” deaths; therefore the “estimated” deaths must still be alive.

---

Is there any visible “Excess” in the Mortality Rate for 2020?

The slight rise in mortality rate for those aged 90+ should be viewed in the context that the 2020 life expectancy in Canada is 81.97.³ In my "Emergency Room Physician" opinion, any outcomes past age 90 are hard to predict. A cold winter, a bad snowstorm or a contagious gastroenteritis running through a nursing home can easily tip anyone over the age of 90 over the edge. In Canada, the proportion of population aged 90 and over is 0.00887.⁴ A slight rise in mortality for less than 1% of the population somehow causing a 5.7% increase in Canada's "excess elderly mortality" is quite a stretch when it comes to "reasonable" estimations.⁵ This is especially true when there were steady or falling mortality rates for the elderly from ages 60-89 who made up 23.9% of the Canadian population in 2020.⁶

On a side note: In the ER, I did not encounter any major life extending advances in medical care of the elderly from 2010 to 2020. Generally speaking, advances in care in one age group, say 90 and over, would also apply to younger age groups in the elderly category as well. Given that mortality rates look unchanged for all ages under 80 from 2010-2020, it looks like there were not any significant medical advances in the care of the elderly despite the slight fall in mortality for those aged 90+ between 2018 and 2019.

On the topic of lockdowns somehow preventing what would have been worse mortality; my own observations having worked throughout 2020 was that neglect appeared to harm as many or more elderly than COVID ever did. This is because visits from family are a large part of people’s lives in nursing homes. Family visits get the elderly out of bed, outside and moving. Without regular family contact, depression often sets in, and the elderly aren’t as mobile. Decreased activity can lead to more bladder infections, bed sores and blood clots from poor circulation. In the younger population, particularly as the lockdowns dragged on, I also observed an increase in substance abuse and suicidality in the ER. Bankruptcies and economic stresses had a noticeable effect on men and women in the prime of their lives. What surprised me was despite these other harms, there was an absence of an increased total mortality in 2020.

---

This next Section is for those interested in Mathematics.

How could the salaried government statisticians get their “Fact Sheet” so wrong?

Did they make a mistake in calculating “excess deaths”?

Lets look at how they did their calculations.

https://web.archive.org/save/https://www.statcan.gc.ca/en/statistical-programs/document/3233_D5_V1

(I always leave a web.archive.org link just in case the government statistics bureau decides to change their numbers. Interestingly, Statistics Canada says they may revise their data at any time.)

It looks like they calculated Excess Mortality by subtracting Actual Morality from Expected Morality.

Er, I meant: Excess Mortality = Actual Mortality - Expected Mortality.

Their equation seems reasonable so far…

Well then, how did they calculate “Expected Mortality"?

1. Crystal Ball?

2. Random number generator?

3. Mathematical Model?

This fine print is from the statistics Canada website:

Estimating expected mortality

The model used to estimate the expected number of deaths is based on a quasi-Poisson regression model fit to weekly death count data. Adapted from an infectious disease detection algorithm developed by Farrington et al.,^{Footnote 9} which has been largely utilized in the context of mortality surveillance in recent years^{Footnote 10}. Later modifications to the algorithm, originally implemented by Noufaily et al.^{Footnote 11} and further expanded by Salmon et al.,^{Footnote 12} that aim at addressing certain limitations of the model were also adopted in this implementation.

The model was implemented in the R programming language with the use of the surveillance package,^{Footnote 12} and was applied to weekly^{Footnote 13} death counts (all-cause) spanning a selected reference period of approximately four years (2016-2019). Historical counts are a combination of published death data from the Canadian Vital Statistics Death Database (2016-2018) and provisional death counts (2019) coming from the National Routing System (NRS). Estimates of expected deaths are produced for all weeks of 2020 up until the week ending July 4, 2020.

An overdispersed Poisson generalized linear model with a linear time trend and a seasonal factor is fit to the data. The seasonal component aims to represent the expected pattern across weeks that repeats from year-to-year, and consists of a zero-order spline term with 11 knots, representing 10 distinct periods within a given year.^{Footnote 14} The 10 periods are split between a single 7-week period corresponding to the current week being estimated and the 3 preceding and subsequent weeks, and 9 other 5-week periods corresponding to the rest of the year.

The model can be expressed using the following log-linear configuration:

log μt=α+βt+γc(t)

where μt is the expectation of the count in week t, β is the coefficient corresponding to the linear time trend, and γc(t) the seasonal factor for week t, with c(t) indicating the period in the year that week t belongs to. ^{Footnote 12}

The quasi-Poisson model relaxes the Poisson assumption that the variance must equal the mean. Instead, E(yt)=μt, and Var(yt)=ϕtμt, where the overdispersion parameter ϕ is estimated from the model using the formula:

ϕ^=max1n-p∑i=1nwi(yi-μ^i)2μ^i,1

where n is the number of weeks used in the baseline, and p the number of parameters in the model. A value of ϕ=1 implies no overdispersion (regular Poisson model), and ϕ<1 implies underdispersion (a rare occurrence, hence the condition on ϕ^). A weight w is assigned to each of the historical observations, based on the value of its standard deviation in an unweighted model. This reduces the influence of potential outliers on the estimation of the expected counts and corresponding prediction interval.

Finally, a 95% prediction interval is computed for the expected count in week t by assuming that the count follows a negative binomial distribution with mean μt and size parameter set to μt⁄(ϕt-1).

It looks like they chose Mathematical Model! But how come their results were so far from reality? How can they say 16,333 excess deaths when in actuality, the 2020 mortality rate looks unchanged or lower than previous years?

Lets look closer at two particular things they mentioned:

1. "Adapted from an infectious disease detection algorithm developed by Farrington et al.,^{Footnote 9} which has been largely utilized in the context of mortality surveillance in recent years ^{Footnote 10}. "

2. The quasi-Poisson model relaxes the Poisson assumption that the variance must equal the mean. Instead, E(yt)=μt, and Var(yt)=ϕtμt, where the overdispersion parameter ϕ is estimated from the model using the formula:

Adapted from an "Infectious disease detection algorithm" ? Really? You’re kidding right?

How could a “detection” algorithm apply to “estimating” total mortality from all causes?

What we are looking for is “excess” death by “estimating” expected death. How does a “detection” algorithm apply to “estimation”? “Detection” algorithms often exaggerate small changes to maximize early detection of threats, such as infections, underwater mines, and INCOMING NUCLEAR MISSILES. We are trying to accurately estimate population deaths, not provide an early warning “detection” of aerial projectiles. Why start off by using the wrong algorithm? Are they stupid? Or is this intentional?

Next they claim to use a "quasi-Poisson model"? Is that like “quasi-mathematics”? Quasi theorums made from “quasi” proofs? (“Oh my! The numbers didn’t really work out the way we wanted, so we just added some variables and undefined feelings to the “Poisson model”. Please trust us, it’s still mathematically correct.” If I didn’t actually pay taxes towards this trash, it would be funny, like a mathematical joke. i.e. “negative 0”.)

"The quasi-Poisson model relaxes the Poisson assumption that the variance must equal the mean." How much "relaxing" did they do? Did they relax just a little? Like 1+1 = 2.1. Or did they “relax” a lot like 1+1 = 10,000? Seriously. wtϕ?

(I have to ask. Are there no more consequences for wrong answers these days? Do students still get University diplomas when they learn nothing?)

If I say “relaxing” Poisson into “quasi-Poisson” is the same as lying, is that an exaggeration?

Is a “Fact Sheet” with an “estimated” 5.7% excess mortality, a lie?

Don’t take my word for it. Compare Canada.ca’s 5.7% “quasi-Mathematics” with reality:

Do you see excess deaths?

---

Let these experts know what you think.

https://www.statcan.gc.ca/en/start

• The Honourable François-Philippe Champagne

  • Minister of Innovation, Science and Industry

• Anil Arora

  • Chief Statistician of Canada

    

1. Nagase, DY. Self extinguishing paradigms in thought. (In progress) b

2. https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.15&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 60-64

https://web.archive.org/web/20230205145358/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.15&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.16&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 65-69

https://web.archive.org/web/20230205145459/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.17&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.17&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 70-74

https://web.archive.org/web/20230205145459/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.17&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.18&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 75-79

https://web.archive.org/web/20230205145548/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.18&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.19&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 80-84

https://web.archive.org/web/20230205145632/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.19&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.20&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 85-89

https://web.archive.org/web/20230205145730/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.20&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.21&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

Ages 90 and Over

https://web.archive.org/web/20230205145834/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310039201&pickMembers%5B0%5D=2.21&pickMembers%5B1%5D=3.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2020&referencePeriods=20100101%2C20200101

3. https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310011401

https://web.archive.org/save/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310011401

4. https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1710000501&pickMembers%5B0%5D=1.1&pickMembers%5B1%5D=2.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2022&referencePeriods=20100101%2C20220101

https://web.archive.org/web/20230207022635/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1710000501&pickMembers%5B0%5D=1.1&pickMembers%5B1%5D=2.1&cubeTimeFrame.startYear=2010&cubeTimeFrame.endYear=2022&referencePeriods=20100101%2C20220101

5. https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310011401

https://web.archive.org/web/20230109014912/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1310011401

6. https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1710000501&pickMembers%5B0%5D=1.1&pickMembers%5B1%5D=2.1&cubeTimeFrame.startYear=2020&cubeTimeFrame.endYear=2020&referencePeriods=20200101%2C20200101

https://web.archive.org/save/https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1710000501&pickMembers%5B0%5D=1.1&pickMembers%5B1%5D=2.1&cubeTimeFrame.startYear=2020&cubeTimeFrame.endYear=2020&referencePeriods=20200101%2C20200101